C7.2 – CRITERI DI PROGETTAZIONE E MODELLAZIONE

C7.2. CRITERI GENERALI DI PROGETTAZIONE E MODELLAZIONE
Questo paragrafo della norma illustra i criteri generali di progettazione e modellazione, indicando le caratteristiche generali che le costruzioni devono possedere per conseguire un comportamento dinamico ottimale in presenza di azioni sismiche, con particolare riguardo alle condizioni di regolarità (§7.2.1). La norma tratta, con le modalità in essa specificate, gli elementi strutturali, gli elementi non strutturali e gli impianti, dedicando attenzione specifica a ciascuna delle tre componenti, per ciascuno stato limite e, dunque, per il corrispondente valore dell’azione sismica, così da consentire il raggiungimento dei rispettivi livelli prestazionali definiti in fase di progettazione.
Per quanto riguarda i sistemi strutturali (§7.2.2), la norma distingue, preliminarmente, tra comportamento dissipativo e comportamento non dissipativo, lasciando libero il progettista di scegliere tra i due e, nel caso in cui opti per il comportamento dissipativo, fornendo i principi, le modalità operative e le regole pratiche per conseguire i livelli di duttilità prefissati.

C7.2.1. CARATTERISTICHE GENERALI DELLE COSTRUZIONI
Regolarità
La regolarità strutturale è finalizzata a favorire, anche in campo inelastico, un comportamento della costruzione e delle sue membrature il più possibile uniforme e tale da evitare concentrazioni di sforzi.
In generale, un edificio può dirsi regolare in pianta e in altezza quando il suo comportamento dinamico sia governato principalmente da modi di vibrare traslazionali lungo le sue direzioni principali e quando tali modi siano caratterizzati da spostamenti crescenti, all’incirca linearmente, con l’altezza.
Con riferimento al §7.2.1 delle NTC le condizioni a) e b) di regolarità in pianta sono sintetizzate nella figura C7.2.1, la condizione g) di regolarità in elevazione è sintetizzata nella figura C7.2.2 e riferita al caso in cui, in una stessa direzione, siano presenti restringimenti in elevazione ad entrambe le estremità; in tal caso il limite del 10% della dimensione corrispondente all’orizzontamento immediatamente sottostante è da intendersi per ciascuno dei due rientri, mentre il limite del 30% della dimensione corrispondente al primo orizzontamento è da intendersi per la somma dei due.
Figura C7.2.1 – Condizioni di regolarità in pianta
Figura C7.2.2 –Condizioni di regolarità in elevazione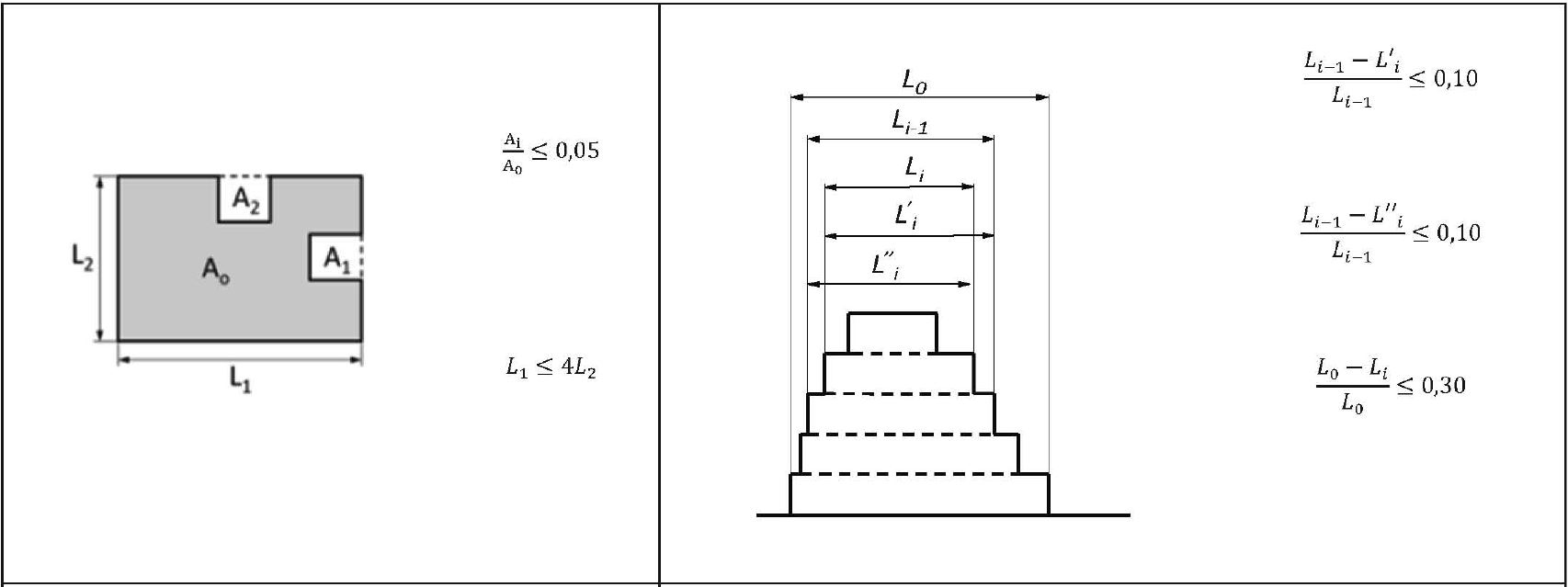
Nel caso in cui in un edificio, immediatamente al di sopra della fondazione, sia presente un basamento, di uno o più piani, con caratteristiche tali da poter essere considerato alla stregua di una struttura scatolare rigida, le NTC specificano che, per valutare la regolarità in altezza, si può far riferimento alla sola parte della struttura che si sviluppa al di sopra del basamento. Tale indicazione tende a escludere la fondazione scatolare rigida dall’individuazione del comportamento strutturale, a condizione che ad essa venga assicurato un comportamento non dissipativo, indipendentemente dallo stato limite considerato².

²Questo requisito è essenziale perché le eventuali plasticizzazioni nella fondazione scatolare altererebbero i rapporti di rigidezza con la sovrastruttura, con la conseguenza di non poter assicurare il soddisfacimento dei criteri di regolarità in elevazione posti a base della progettazione.

Distanza tra costruzioni contigue
Tra costruzioni contigue la norma impone la verifica degli spostamenti massimi per evitare fenomeni di martellamento; tale verifica deve essere eseguita attraverso un calcolo diretto degli spostamenti assicurando, in ogni caso, che la distanza tra le costruzioni non risulti inferiore al valore minimo stabilito dalla norma.
L’eventualità in cui non si possano eseguire calcoli specifici va riferita solo al caso di progettazione di nuova costruzione in adiacenza a costruzioni esistenti.

C7.2.2. CRITERI GENERALI DI PROGETTAZIONE DEI SISTEMI STRUTTURALI
Le prescrizioni normative sono volte a garantire che l’organismo strutturale sia dotato di sistemi resistenti disposti almeno secondo due direzioni distinte, capaci di garantire un’adeguata resistenza e rigidezza nei confronti sia dei moti traslazionali, sia dei moti torsionali, dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza dell’intera struttura o anche solo di una sua porzione, che tendono a sollecitare i diversi elementi strutturali in maniera non uniforme.
Al riguardo, nel caso degli edifici, sono da preferirsi configurazioni strutturali in cui i principali elementi resistenti all’azione sismica sono distribuiti nelle zone perimetrali, così da massimizzare la rigidezza torsionale della costruzione. Per sfruttare al meglio la rigidezza torsionale conseguita nel modo suddetto è necessario che gli orizzontamenti, ai fini della ripartizione degli effetti delle componenti orizzontali dell’azione sismica, tra gli elementi verticali che li sostengono, funzionino da diaframma rigido nei modi specificati al § 7.2.6 delle NTC.
Per quanto riguarda gli effetti della componente verticale dell’azione sismica, nel § 7.2.2 sono indicati gli elementi e le tipologie costruttive che maggiormente risentono delle accelerazioni verticali indotte dal sisma, nonché i livelli di pericolosità per i quali tale componente deve essere considerata nel progetto. Per gli elementi soggetti a tali azioni e per quelli di supporto dei medesimi è ammesso l’uso di modelli parziali che tengano conto della rigidezza degli elementi adiacenti.
In generale non si tiene conto della variabilità spaziale del moto sismico e si adotta per esso una rappresentazione di tipo “puntuale”, quale è quella che prevede l’utilizzo degli spettri di risposta adottando un unico valore di accelerazione del suolo per tutti i punti di contatto tra esso e la struttura.
Quando, per l’estensione del sistema di fondazione, non è realistica l’ipotesi che l’intera costruzione sia soggetta ad una eccitazione sismica uniforme, è necessario considerare la variabilità spaziale del moto di cui al § 3.2.4 delle NTC.
Le NTC distinguono tra due tipi di comportamento strutturale:
a) non dissipativo;
b) dissipativo.
Specificando, per ciascun comportamento, i corrispondenti criteri di modellazione dell’azione sismica e della struttura.
Le NTC consentono al progettista di optare per uno dei due comportamenti, in relazione al particolare problema progettuale. Il comportamento strutturale non dissipativo (a) richiede che la struttura abbia resistenza tale da rimanere in campo sostanzialmente elastico per tutti gli stati limite considerati. Il comportamento strutturale dissipativo (b) si basa sulla duttilità e presuppone dunque l’accettazione del danneggiamento strutturale come strategia di protezione passiva per i terremoti di progetto agli stati limite ultimi.
Nel caso di comportamento strutturale non dissipativo (a) la risposta sismica della struttura dipende, essenzialmente, dalle sue caratteristiche di rigidezza e resistenza; in caso di comportamento strutturale dissipativo (b), dalle caratteristiche di rigidezza, resistenza e dalla capacità di sviluppare deformazioni cicliche in campo plastico (duttilità).
L’insieme delle prescrizioni contenute nelle NTC, finalizzate al conseguimento dei prefissati livelli di duttilità, costituisce la “progettazione in capacità”.
Quando si opta per il comportamento non dissipativo (a) le azioni sismiche di progetto sono più elevate, ma la duttilità necessaria è molto contenuta e dunque non è richiesta la progettazione in capacità e l’adozione dei dettagli costruttivi riportati al Capitolo 7; quando, invece, si opta per il comportamento dissipativo (b), le azioni sismiche di progetto sono minori, ma la duttilità necessaria è più elevata e dunque è richiesta la progettazione in capacità e l’adozione di dettagli costruttivi specifici.
Il comportamento dissipativo (b), ammette, in generale, un danneggiamento della costruzione, eventualmente anche esteso ma controllato, per i livelli di azione relativi a SLV e SLC e un possibile danneggiamento, di entità comunque limitata, per lo SLD.
A ciò fanno eccezione le strutture dotate di isolamento alla base, per le quali anche i requisiti riferiti agli stati limite ultimi vengono conseguiti evitando significative escursioni in campo plastico degli elementi strutturali della sovrastruttura e della sottostruttura ( si veda il § 7.10.2 delle NTC).
Nelle costruzioni dissipative e prive di specifici dispositivi antisismici o di controllo delle vibrazioni, ai fini di un buon comportamento dissipativo d’insieme, le deformazioni inelastiche devono essere distribuite nel maggior numero possibile di elementi duttili per contenere l’entità delle plasticizzazioni.
In funzione della tecnologia costruttiva e dei materiali utilizzati, è dunque possibile separare i meccanismi deformativi fragili o scarsamente dissipativi, dai meccanismi duttili ai quali è invece possibile associare, mediante adeguati accorgimenti, significativa capacità di dissipare energia .
La progettazione del comportamento dissipativo, effettuata secondo le NTC, è mirata a garantire l’attivazione dei meccanismi deformativi, locali e globali, che concentrino la domanda di duttilità negli elementi più duttili (ad es. le travi) invece che negli elementi meno duttili (ad es. le pareti o i pilastri, particolarmente quelli soggetti a sforzi normali di compressione rilevanti) e che impediscano l’attivazione di meccanismi fragili ( ad es. rottura a taglio di pareti, travi o pilastri, rottura di nodi trave-pilastro), sia locali sia globali, o globalmente instabili.
La duttilità d’insieme della costruzione si ottiene, in definitiva, individuando gli elementi ed i meccanismi resistenti ai quali affidare le capacità dissipative e localizzando, all’interno del sistema strutturale, le zone in cui ammettere la plasticizzazione, in modo da ottenere un meccanismo deformativo d’insieme stabile, che coinvolga il maggior numero possibile di fonti di duttilità locale.
Nell’ambito del comportamento strutturale dissipativo, il progettista può decidere di conseguire la Classe di Duttilità Alta (CD”A”), a elevata capacità dissipativa, oppure la Classe di Duttilità Media (CD”B”), a media capacità dissipativa, rappresentando dunque le lettere “A” e “B” una mera tipizzazione.
La scelta della CD”A” rispetto alla CD”B” si traduce in un’ulteriore riduzione delle azioni di progetto, ma implica richieste di duttilità più elevate e, in generale, un maggiore onere in termini di dettagli costruttivi.
La norma definisce i criteri progettuali per conseguire il livello di duttilità prefissato; l’insieme di tali criteri costituisce la “progettazione in capacità”.
In particolare, al fine di garantire il comportamento duttile locale e globale, fatta la distinzione tra elementi/meccanismi fragili e duttili, su ciascun elemento si determina:
- la domanda in termini di resistenza, stabilendo, in base a considerazioni di equilibrio, una “gerarchia delle resistenze” tra elementi/meccanismi fragili (più resistenti) e elementi/meccanismi duttili (meno resistenti);
- la domanda in termini di duttilità nelle zone destinate a plasticizzarsi, cui deve essere garantito un comportamento inelastico dissipativo e stabile in condizioni cicliche (duttile).
Si progettano, quindi, in termini di resistenza e/o duttilità, le corrispondenti capacità.
Per conseguire gli obiettivi insiti nella progettazione in capacità, si impiegano fattori di sovra resistenza γ_Rd, opportunamente differenziati tra le due classi di duttilità³.
Le NTC prescrivono che il comportamento duttile vada perseguito sia a livello locale sia a livello globale. A tal fine viene prescritto un valore di sovra resistenza γ_Rd ≥1,25 per i meccanismi globali fragili rispetto ai meccanismi globali duttili.
Per una struttura alla quale si richiede un comportamento duttile e che abbia al suo interno pareti di controventamento tozze (particolarmente suscettibili di rottura a taglio) e talai duttili, ciò comporta l’assunzione di γ_Rd locali sulle pareti tali da assicurare che, per attivare un meccanismo globale che veda la rottura a taglio delle pareti, occorrano azioni sismiche maggiori, almeno di un fattore 1,25, delle azioni richieste per attivare il meccanismo a telaio⁴.
Al riguardo è bene chiarire che, nel caso di strutture a telaio, l’applicazione della progettazione in capacità è finalizzata, a livello globale, ad impedire l’attivazione di meccanismi instabili di piano, a livello locale, a controllare le plasticizzazioni nei pilastri senza escluderle in assoluto.
Proprio per questa ragione, in accordo con la UNI ENI1998, per la pressoflessione di pilastri o colonne si adotta un fattore di sovraresistenza γ_Rd unico e pari a 1,3, sia per la CD”A” sia per la CD”B”. Per lo stesso motivo, non essendo possibile escludere che, durante l’evento sismico, si abbiano plasticizzazioni in alcuni pilastri, alle zone di estremità di tutti i pilastri primari deve essere garantito un comportamento dissipativo.
i valori dei fattori di sovra resistenza γ_Rd, distinti per tipologia strutturale e Classi di Duttilità, sono riportati nella Tabella 7.2.I delle NTC.
I principi della progettazione in capacità sono alla base della progettazione antisismica e si applicano ogni qual volta si voglia favorire un determinato comportamento strutturale a livello sia locale sia globale.
Analogamente, se si vuole valutare la massima domanda a taglio in un elemento strutturale, si determina, in base a semplici considerazioni di equilibrio, il valore del taglio in equilibrio con le azioni esterne (ad es. il carico verticale distribuito in una trave) e con la capacità a flessione (momenti resistenti) nelle sezioni di estremità, analizzando, per quanto riguarda i versi delle sollecitazioni, le diverse situazioni possibili in condizioni sismiche.

³I fattori di sovraresistenza tengono conto delle incertezze nella determinazione delle resistenze, dovute ai materiali, alla geometria, al modello di calcolo, ecc; tali fattori, almeno pari all’unità, vengono utilizzati per maggiorare la domanda in termini di resistenza (e di conseguenza la corrispondente capacità) degli elementi/meccanismi fragili di cui si vuole impedire l’attivazione. Essi includono, oltre alle incertezze dette, anche l’incertezza sulle capacità dell’elemento duttile di cui si vuole favorire la plasticizzazione ed hanno lo scopo di ridurre la probabilità di attivazione delle rotture/meccanismi indesiderati.

⁴Per evitare che, in forza di questa prescrizione, il progettista sia obbligato a produrre più modelli di calcolo confrontandoli poi sistematicamente, le NTC richiedono che la verifica avvenga “anche solo su base deduttiva a partire dai fattori di sovra resistenza R_d da utilizzare nella progettazione in capacità a livello locale”.

C7.2.3. CRITERI DI PROGETTAZIONE DI ELEMENTI STRUTTURALI “SECONDARI” ED ELEMENTI COSTRUTTIVI NON STRUTTURALI
Elementi Secondari⁵
Gli elementi strutturali secondari devono essere in grado, nella condizione deformata più sfavorevole, di mantenere la loro capacità portante nei confronti dei carichi verticali tenendo conto, quando necessario, delle non linearità geometriche nei modi specificati nel § 7.2.3 delle NTC, non subiscono plasticizzazioni, per questi ultimi possono essere adottati i particolari costruttivi prescritti al Capitolo 4; in caso contrario valgono le prescrizioni del Capitolo 7.

⁵Per facilitare la progettazione in situazioni oggettivamente difficili quali, ad esempio, quelle che si presentano quando, per ragioni architettoniche, alcuni elementi debbano avere dimensioni nettamente maggiori di quelle che sarebbero loro richieste dal progetto strutturale, le NTC consentono di trattare tali elementi come elementi secondari e dunque di trascurare la loro rigidezza e resistenza alle azioni orizzontali. Tale semplificazione è condizionata al rispetto di alcune condizioni precisate nelle norme.

Elementi costruttivi non strutturali
Le NTC classificano gli elementi costruttivi non strutturali in due gruppi:
1) elementi con rigidezza, resistenza e massa tali da influenzare in maniera significativa la risposta strutturale;
2) elementi che influenzano la risposta strutturale solo attraverso la loro massa, ma sono ugualmente significativi ai fini della sicurezza e/o dell’incolumità delle persone.
Ai fini anche della determinazione della domanda sismica, per il primo gruppo di elementi non strutturali, si potrà introdurre, in relazione al tipo di verifica e di analisi da effettuarsi, nel modello strutturale globale oltre alla massa degli elementi che viene sempre considerata anche la loro rigidezza descrivendone le condizioni di vincolo alla struttura.
Per il secondo gruppo di elementi non strutturali, ottenuta la risposta in accelerazione della struttura a ciascun piano, la si può assimilare ad una forzante esterna da applicare all’elemento non strutturale, così ricavando la domanda sismica su di esso.
La verifica degli elementi non strutturali, degli impianti o, per le costruzioni di muratura, dei meccanismi locali richiede una corretta valutazione dell’input sismico; il moto alla base dell’edificio è infatti filtrato dalla risposta della costruzione, in relazione alle sue caratteristiche dinamiche (frequenze proprie) e alla quota alla quale gli elementi soggetti a verifica sono collocati (forme modali); a tal fine risulta utile la seguente definizione di spettri di risposta di piano.

Spettri di risposta di piano
Gli spettri di risposta di piano rappresentano un modello per la valutazione dell’azione sismica in un predeterminato punto della struttura. Diverse formulazioni, più o meno approssimate, possono essere utilizzate. Nel seguito si riportano alcuni possibili metodi di calcolo, è ammesso l’uso anche di altre formulazioni purché di comprovata e documentata validità.
Gli spettri di risposta di ciascun piano possono essere determinati, a partire dalla risposta in accelerazione della struttura alla quota considerata, nell’ipotesi semplificativa che la struttura possa essere assunta come una forzante armonica per l’elemento non strutturale, portando in conto le amplificazioni dovute agli effetti dinamici sul singolo elemento non strutturale, legate al suo periodo di oscillazione e al suo coefficiente di smorzamento nonché alle corrispondenti caratteristiche della struttura.
Nella formula [7.2.1], il parametro Sa rappresenta appunto l’accelerazione massima (risposta), normalizzata rispetto a quella di gravità, che l’elemento non strutturale subisce durante il sisma, per lo stato limite considerato. L’inviluppo dei valori assunti da S_a al variare del periodo proprio T_a, a un generico piano della costruzione, costituisce lo spettro di risposta di quel piano.
L’accelerazione del piano j-esimo della struttura relativa al modo i-esimo è data dalla relazione:


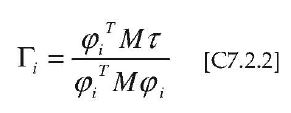
Il vettore τ è il vettore di trascinamento corrispondente alla direzione del sisma considerata; il vettore φ_i è la forma modale del modo i-esimo normalizzata al valore massimo; la matrice M è la matrice di massa del sistema reale.
L’accelerazione dell’elemento non strutturale al piano considerato, nella direzione considerata, per il modo i-esimo, è data, dunque, dall’equazione: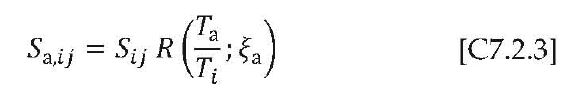

dove R, fattore di amplificazione dell’elemento non strutturale, è funzione del coefficiente di smorzamento ξ_a dell’elemento e del rapporto tra il periodo dell’elemento T_a e il periodo del modo i-esimo della struttura T_i, e vale: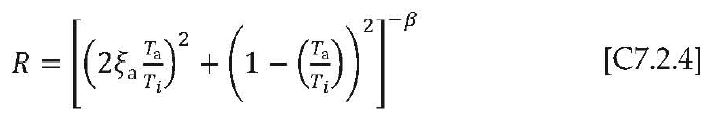

L’eq. C7.2.3 rappresenta la risposta del singolo elemento non strutturale di periodo T_a, posto al piano j-esimo, per effetto del modo di vibrare i-esimo della struttura e tiene conto attraverso il coefficiente β (variabile tra 0,4 e 0,5) dell’accoppiamento tra ciascun modo di vibrare della struttura e il modo proprio dell’elemento non strutturale. La risposta totale si ottiene combinando opportunamente le risposte relative ai diversi modi, ad es. attraverso la regola SRSS.
La norma consente infine di ridurre la domanda sismica Sa su ciascun elemento non strutturale attraverso uno specifico fattore di comportamento q_a. In tabella [C7.2.I] sono riportati i valori di q_a utilizzabili per le tipologie ricorrenti di elementi non strutturali.
Tabella C7.2.I – Valori di q_a per elementi non strutturali

È opportuno che il progettista, in base a considerazioni specifiche sulla risposta strutturale dell’elemento, indichi espressamente il gruppo attribuito a ciascun elemento non strutturale e il tipo di modellazione adottata. Nell’attribuzione del gruppo è opportuno ricordare che uno stesso elemento strutturale, ad esempio una tamponatura robusta, può appartenere al gruppo 1 per azioni sismiche nel proprio piano medio e al gruppo 2 per azioni sismiche ortogonali al proprio piano medio e tenere opportuno conto di ciò nel modello di calcolo.
Poiché la risposta degli elementi non strutturali è legata, attraverso il periodo proprio dell’elemento, ai modi di vibrare della struttura, nel valutarne la risposta si deve considerare un intervallo nell’intorno del periodo fondamentale della struttura, che tenga conto, per il limite inferiore dell’intervallo, delle possibili incertezze di modellazione o dell’incremento di rigidezza rispetto al modello di riferimento dovuta agli elementi non strutturali, per il limite superiore dell’intervallo, dell’incremento di periodo dovuto alle plasticizzazioni, da valutarsi in funzione del fattore di comportamento attribuito alla struttura. Lo stesso fattore di comportamento deve essere utilizzato per la valutazione della risposta spettrale inelastica della struttura.

Formulazione semplificata, a diverse quote, per elementi non strutturali, impianti, eventuali meccanismi locali
Nel seguito è fornita una formulazione analitica semplificata, valida per gli elementi non strutturali, per gli impianti e per eventuali meccanismi locali, valida qualunque sia la tipologia della costruzione.
La formulazione analitica semplificata consente di valutare lo spettro di accelerazione S_eZ(T,ξ) ad una quota z significativa per l’elemento non strutturale, l’impianto o il meccanismo locale in esame; la formulazione è basata sulle proprietà dinamiche della struttura principale e sui valori dello spettro di risposta alla base dell’edificio calcolati in corrispondenza dei periodi propri della costruzione.
Questa formulazione consente di tenere conto del contributo fornito da tutti i modi di vibrazione ritenuti significativi; in linea generale devono essere preventivamente individuate le forme di vibrazione (ed i relativi periodi) significative per l’elemento non strutturale, l’impianto o il meccanismo locale in esame, anche in relazione alla sua posizione in pianta (la sommatoria nella formula che segue è estesa a questi modi, identificati dal pedice k):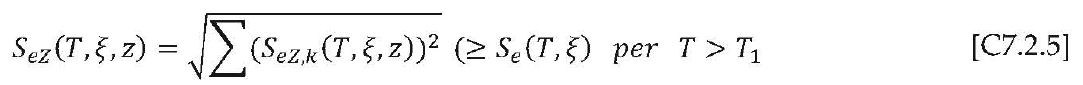




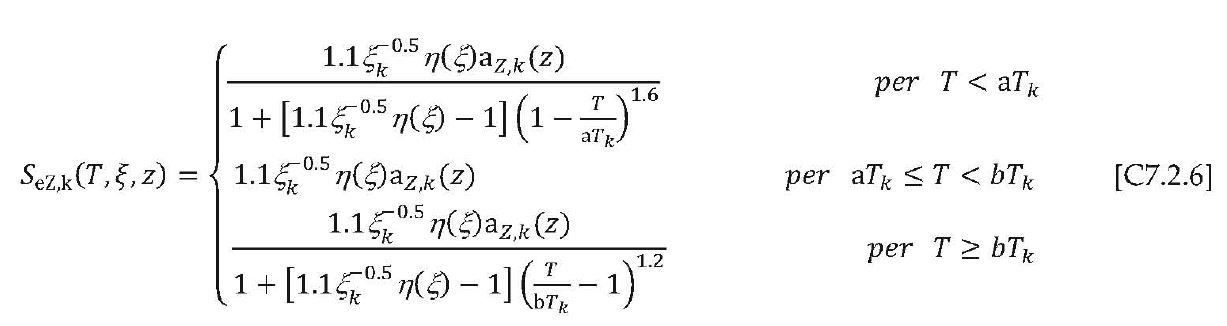
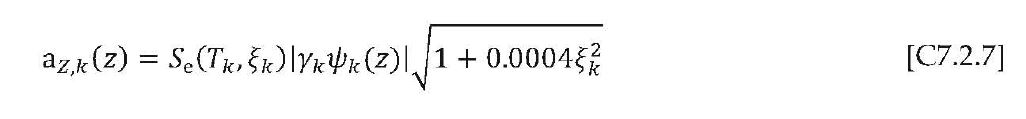
L’accelerazione massima alla quota z è quindi fornita dalla seguente espressione: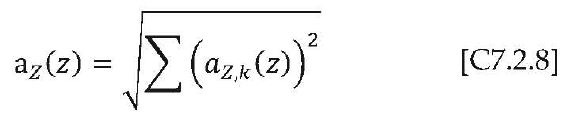

mentre il contributo al picco di accelerazione spettrale in corrispondenza del periodo T_k, fornito dal k-esimo modo, vale:

Nella verifica di meccanismi locali in edifici multipiano è, in genere, sufficiente riferirsi al solo primo modo di vibrare nella direzione di verifica, in quanto è quello che induce la domanda di spostamento più significativa; nel caso in cui si stia eseguendo una verifica globale dell’edificio principale attraverso un’analisi statica non lineare, per il periodo T₁ può essere assunto il periodo elastico T*, dato dalla formula [C7.3.6] riportata nel § C7.3.4.2.
Una valutazione più accurata di T₁ richiederebbe la stima del periodo secante del sistema bilineare, in corrispondenza della domanda di spostamento (v. equazione [C7.3.7] o [C7.3.8]) prodotta dall’accelerazione al suolo che porta allo stato limite il meccanismo locale (procedimento iterativo che tiene conto dello stato di danneggiamento della struttura principale, al raggiungimento dello stato limite da parte del meccanismo locale).
In assenza di tali valutazioni, il periodo T₁ può essere stimato con la formula [7.3.6] del § 7.3.3.2.
Nel caso di strutture con masse distribuite in maniera sostanzialmente uniforme lungo l’altezza, se si assume la prima forma modale lineare e la si normalizza allo spostamento in sommità all’edificio, il coefficiente di partecipazione modale può essere approssimato alla formula:

dove n è il numero dei piani.
Si segnala che gli spettri alle diverse quote sono fortemente influenzati dl livello di non linearità della struttura principale; essi presentano infatti una forte amplificazione in corrispondenza del periodo fondamentale della struttura elastica. Tale amplificazione si riduce considerevolmente quando la struttura entra in campo non lineare. La formulazione proposta considera tale effetto attraverso lo smorzamento viscoso equivalente ξ_k e l’incremento del periodo equivalente T_k.

Formulazione semplificata per costruzioni con struttura a telai
Per le sole costruzioni con struttura intelaiata, in alternativa alle precedenti formulazioni e nell’ipotesi di andamento delle accelerazioni strutturali linearmente crescenti con l’altezza, l’accelerazione massima S_a(T_a) può essere determinata attraverso l’espressione [C7.2.5].
In alternativa all’utilizzo di specifici spettri di risposta di piano e nell’ipotesi di andamento delle accelerazioni strutturali linearmente crescenti con l’altezza, l’accelerazione massima S_a(T_a) può essere determinata attraverso l’espressione [C7.2.5 o 11].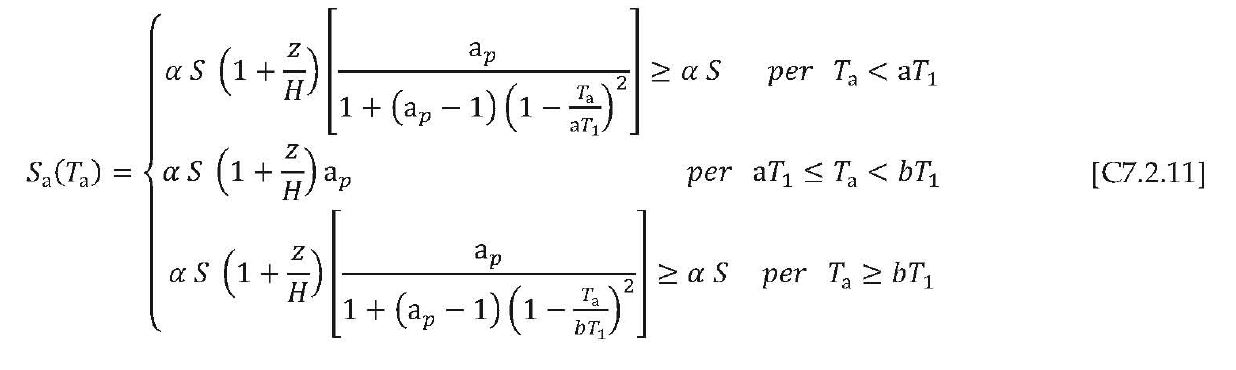


Per le strutture con isolamento sismico si assume sempre z = 0.
Gli spettri di piano, descritti attraverso l’eq. C7.2.11, sono in generale conservativi per un ampio campo di periodi, con particolare riguardo a elementi non strutturali aventi periodo proprio prossimo al periodo fondamentale della costruzione. In particolare i parametri a, b, e a_p sono stati definiti in accordo con il periodo proprio della struttura e calibrati per tener conto dell’elongazione del periodo fondamentale, legata alle non linearità del sistema, e del contributo dei modi superiori.
Figura C7.2.3 – Spettri di risposta di piano per gli elementi non strutturali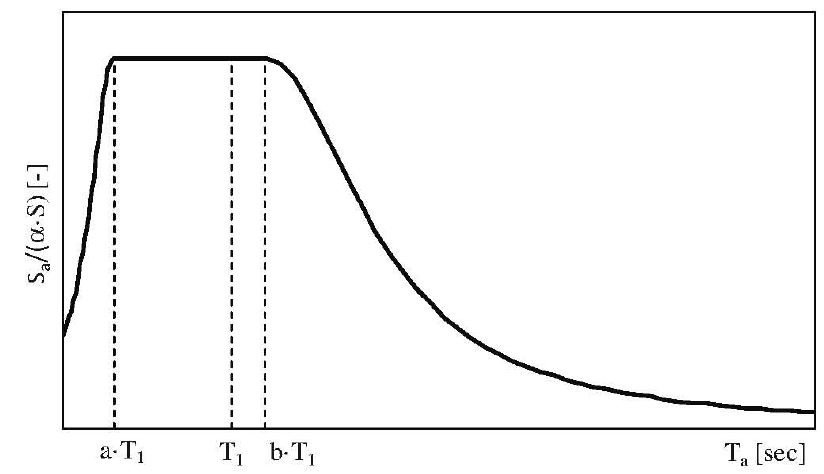

Tabella C7.2.II – Parametri a, b, e a_p in accordo con il periodo di vibrazione della costruzione T₁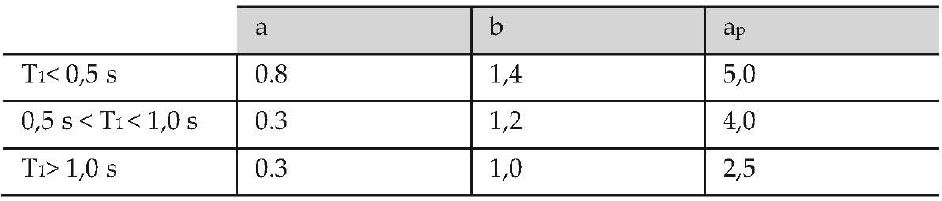

Figura C7.2.4 – Accelerazione massima, normalizzata rispetto ad αS, per i seguenti valori di T₁: (a) T₁ = 0,3s, (b) T₁ = 0,6s, (c) T₁ = 0,9s, (d) T₁ = 1,2s.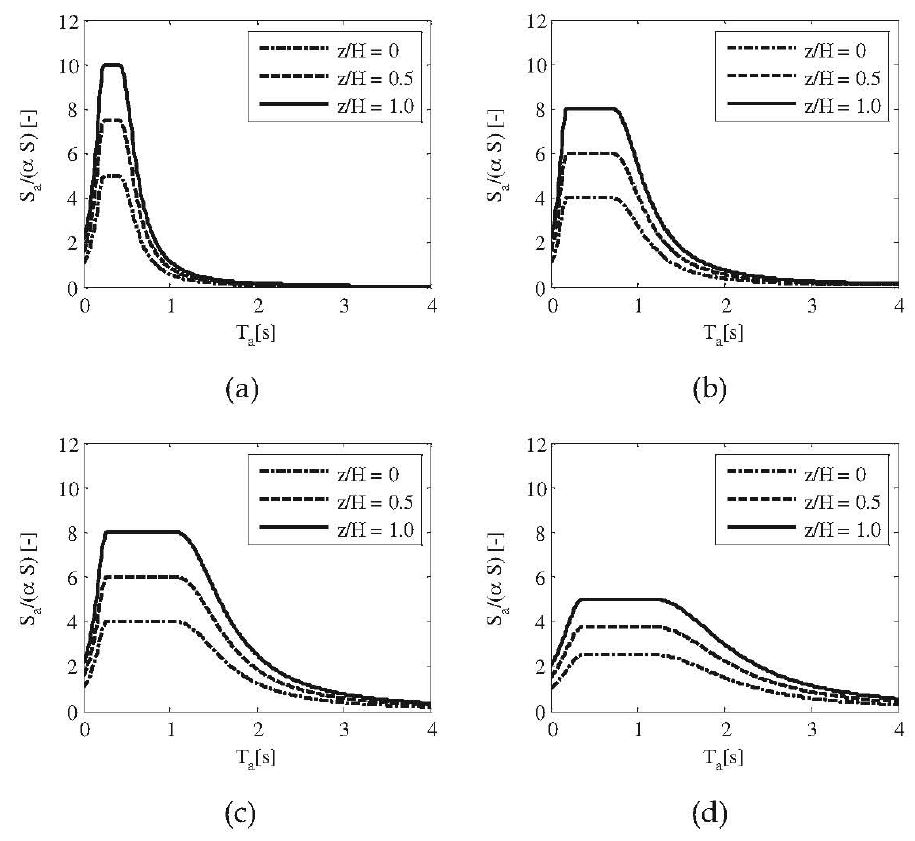

L’approccio seguito per la determinazione degli effetti sugli elementi non strutturali del secondo gruppo può essere utilizzato anche per quelli del primo gruppo, a condizione che la risposta strutturale sia determinata attraverso un modello che includa sia la massa sia la rigidezza degli elementi non strutturali. Ciò può rendersi necessario per quei modelli che non consentano la determinazione diretta della risposta dinamica degli elementi non strutturali.

C7.2.6. CRITERI DI MODELLAZIONE DELLA STRUTTURA E DELL’AZIONE SISMICA
Modellazione della struttura
Gli orizzontamenti devono essere dotati di opportuna rigidezza e resistenza nel piano e essere collegati in maniera efficace alle membrature verticali che li sostengono, affinché possano assolvere la funzione di diaframma rigido ai fini della ripartizione delle forze orizzontali tra le membrature verticali stesse. Particolare attenzione va posta quando abbiano forma molto allungata o comunque non compatta; in quest’ultimo caso, occorre valutare se le aperture presenti, specie se localizzate in prossimità dei principali elementi resistenti verticali, non riducano significativamente la resistenza.
Gli orizzontamenti possono essere considerati infinitamente rigidi nel loro piano se, modellandone la deformabilità nel piano, le variazioni degli spostamenti di tutti i punti appartenenti al piano in esame non differiscono tra loro più del 10%. Tale condizione può ritenersi generalmente soddisfatta nei casi specificati nelle NTC (v. § 7.2.6), salvo porre particolare attenzione quando gli orizzontamenti siano sostenuti da elementi strutturali verticali (per es. pareti) di notevole rigidezza e resistenza.
Quando gli orizzontamenti possono essere considerati infinitamente rigidi nel loro piano, le masse e le inerzie rotazionali di ogni piano possono essere concentrate nel suo centro di gravità.
Ai fini di una corretta valutazione della risposta strutturale, la norma richiede che, nel rappresentare la rigidezza flessionale e a taglio dei singoli elementi di muratura, calcestruzzo, acciaio-calcestruzzo, si tenga conto della fessurazione. La norma prevede che, in assenza di analisi specifiche, la rigidezza degli elementi fessurati non si assunta minore del 50% delle corrispondenti rigidezze non fessurate. Valori minori possono essere assunti a fronte di specifiche valutazioni adeguatamente motivate.
La norma precisa che in ogni caso, nella valutazione della rigidezza degli elementi fessurati, si debba tenere conto dello stato limite considerato⁶ e dell’influenza della sollecitazione assiale permanente.

⁶il coefficiente di fessurazione allo SLD dipende dal fattore di comportamento q, in quanto quest’ultimo condiziona lo stato fessurativo che si riscontra in corrispondenza dei diversi stati limite considerati. Ad esempio, se si adotta per la progettazione allo SLV un fattore di comportamento q di notevole entità, è ragionevole ipotizzare che molti elementi possano essere plasticizzati e che gran parte di essi siano fessurati in maniera estesa; può accadere inoltre che, in corrispondenza di un’azione sismica minore (ad esempio quella corrispondente allo SLD), ci siano già plasticizzazioni ed estese fessurazioni. Se invece la struttura è stata progettata allo SLV per valori ridotti del fattore di comportamento q, è ragionevole ipotizzare che, per azioni sismiche minori quali quelle relative allo SLD, molti elementi siano ancora in campo elastico o siano fessurati in maniera limitata, tenuto sempre conto che la fessurazione si manifesta comunque anche per effetto dei soli carichi verticali. Per gli elementi di calcestruzzo armato la fessurazione degli elementi dipende dalla geometria, dai quantitativi di armatura e dallo stato di sollecitazione; pertanto, per tenerne correttamente conto, si dovrebbe ricorrere a un processo iterativo, che risulterebbe eccessivamente oneroso e, in ogni caso, affetto da numerose incertezze.

Per gli elementi in calcestruzzo armato si può, in maniera semplificata, adottare un coefficiente riduttivo della rigidezza denominato coefficiente di fessurazione α_f, da applicare sia alla rigidezza flessionale sia alla rigidezza a taglio di ciascun elemento. Tale coefficiente è espresso in funzione del carico assiale N e del fattore di comportamento q adottati per la progettazione allo SLV.
Nelle figure C7.2.5 (a) e C7.2.5 (b), q rappresenta il fattore di comportamento, N lo sforzo normale dovuto ai soli carichi verticali nella combinazione sismica, A_c l’area della sezione, f_cd la resistenza a compressione del calcestruzzo.
Figura C7.2.5 – Dipendenza di αf dal carico assiale N e dal fattore di comportamento q.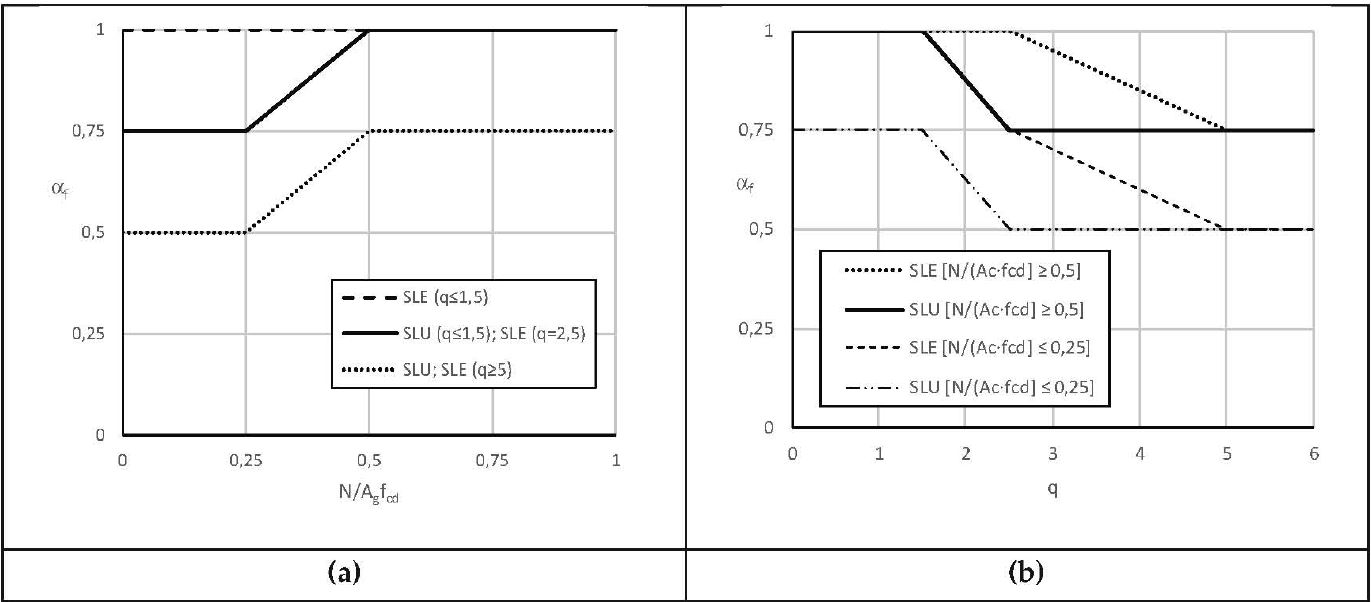

Modellazione dell’azione sismica
Per semplicità di analisi è possibile descrivere la variabilità spaziale del moto e l’aleatorietà dell’effettivo baricentro delle masse e delle rigidezze attraverso lo spostamento del centro di massa dalla sua posizione originaria nella direzione delle due componenti orizzontali e in ambo i versi. In alternativa è consentito (§ 7.3.3) applicare un momento torcente valutato a partire dalla risultante orizzontale della forza agente al piano, determinata come in § 7.3.3.2, moltiplicata per l’eccentricità accidentale⁷ del baricentro delle masse rispetto alla sua posizione di calcolo, determinata come in § 7.2.6.
Nel valutare gli effetti dell’eccentricità accidentale, si dovranno considerare, ovviamente, gli effetti concomitanti delle due componenti dell’azione sismica, utilizzando le regole di combinazione indicate al § 7.3.5.

⁷Si specifica che l’eccentricità accidentale, oltre che per considerare le incertezze legate alla localizzazione delle masse, è una maniera indiretta per tenere conto della variabilità spaziale del moto sismico. A rigore, infatti, si dovrebbe considerare una componente torsionale del trascinamento sismico, sia nelle analisi statiche, sia nelle analisi dinamiche; tradizionalmente, invece, l’azione sismica viene descritta esclusivamente attraverso le due componenti traslazionali orizzontali del moto, cui va aggiunta, ove significativa, la componente verticale.