C7.3. – METODI DI ANALISI E CRITERI DI VERIFICA

INDICE
C7.1. REQUISITI DELLE COSTRUZIONI NEI CONFRONTI DEGLI STATI LIMITE
C7.2. CRITERI GENERALI DI PROGETTAZIONE E MODELLAZIONE

C7.3. METODI DI ANALISI E CRITERI DI VERIFICA
C7.3.1. ANALISI LINEARE O NON LINEARE
C7.3.3. ANALISI LINEARE DINAMICA O STATICA
C7.3.3.1 ANALISI LINEARE DINAMICA
C7.3.3.2 ANALISI LINEARE STATICA
C7.3.4. ANALISI NON LINEARE DINAMICA O STATICA
C7.3.4.1 ANALISI NON LINEARE DINAMICA
C7.3.4.2 ANALISI NON LINEARE STATICA
C7.3.5. RISPOSTA ALLE DIVERSE COMPONENTI DELL’AZIONE SISMICA ED ALLA VARIABILITÀ SPAZIALE DEL MOTO
C7.3.6. RISPETTO DEI REQUISITI NEI CONFRONTI DEGLI STATI LIMITE
C7.3.6.1 ELEMENTI STRUTTURALI (ST)
C7.3.6.2 ELEMENTI NON STRUTTURALI (NS)

C7.4. COSTRUZIONI DI CALCESTRUZZO
C7.5. COSTRUZIONI DI ACCIAIO
C7.6. COSTRUZIONI COMPOSTE DI ACCIAIO-CALCESTRUZZO
C7.7. COSTRUZIONI DI LEGNO
C7.8. COSTRUZIONI DI MURATURA
C7.9. PONTI
C7.10. COSTRUZIONI CON ISOLAMENTO E/O DISSIPAZIONE
C7.11. OPERE E SISTEMI GEOTECNICI

C7.3. METODI DI ANALISI E CRITERI DI VERIFICA
C7.3.1. ANALISI LINEARE O NON LINEARE
Quando nella progettazione allo SLV si adottano fattori di comportamento q elevati (mediamente superiori a 2,5), può accadere che le ordinate dello spettro SLD superino le corrispondenti ordinate dello spettro SLV.
Ciò implica, per le strutture in classe d’uso 1 e 2, per le quali allo SLD è richiesta dalle NTC la sola verifica in termini di rigidezza (RIG, si veda § 7.3.6) che gli elementi strutturali possano plasticizzarsi anche per eventi sismici relativamente frequenti, quali quelli corrispondenti allo SLD. In questo caso, se si vuole garantire l’assenza di danno strutturale allo SLD, è necessario effettuare, allo stesso SLD, anche la verifica in termini di resistenza (RES) oppure si può ridurre il fattore di comportamento da adottare nella progettazione allo SLV in modo tale da mantenere le ordinate dello spettro SLD al di sotto delle corrispondenti ordinate dello spettro SLV.
Il nuovo fattore di comportamento q’ può essere ottenuto, per ciascuna direzione, dalla relazione C7.3.1:

Dove: q_ND è il fattore di comportamento non dissipativo definito dall’espressione [7.3.2] della norma; T1 è il periodo del primo moto traslazionale nella direzione considerata; S_e,SLV(T₁) e S_e,SLD(T₁) sono, rispettivamente, la risposta spettrale elastica allo SLV e allo SLD, relative al periodo T₁.
Gli effetti torsionali accidentali, sia nel caso di analisi lineare statica o dinamica o non lineare statica o dinamica, vengono considerati nel modo previsto al § 7.2.6 delle NTC.

C7.3.3. ANALISI LINEARE DINAMICA O STATICA
C7.3.3.1 ANALISI LINEARE DINAMICA^8
8L’analisi lineare dinamica, così come presentata nelle NTC, avviene in tre passi fondamentali:
1) determinazione dei modi di vibrare “naturali” della struttura (analisi modale);
2) calcolo degli effetti dell’azione sismica, rappresentati dallo spettro di risposta di progetto, per ciascuno dei modi di vibrare individuati;
3) combinazione degli effetti relativi a ciascun modo di vibrare per valutare la risposta complessiva.
L’analisi modale consiste nella soluzione delle equazioni del moto della struttura, considerata elastica, in condizioni di oscillazioni libere (assenza di forzante esterna) e nella individuazione di particolari configurazioni deformate che costituiscono i modi naturali di vibrare di una costruzione.
Questi modi di vibrare sono una caratteristica propria della struttura, in quanto sono individuati in assenza di forzante, e sono caratterizzati da un periodo proprio di oscillazione T e da un fattore di smorzamento convenzionale ξ, nonché da una forma. Tranne che per casi particolari, quali ad esempio quelli di costruzioni dotate di sistemi di isolamento e dissipazione, si assume che i modi di vibrare abbiano tutti lo stesso valore del fattore di smorzamento convenzionale ξ ossia ξ = 5%. Qualunque configurazione deformata di una struttura (e lo stato di sollecitazione a tale deformata connesso), può essere ottenuta come combinazione di deformate elementari, ciascuna con la forma di un modo di vibrare.
Ovviamente, in funzione dell’azione che agisce sulla costruzione, alcuni modi di vibrare avranno parte più significativa di altri nella descrizione della configurazione deformata. La massa partecipante di un modo di vibrare esprime la quota parte delle forze sismiche di trascinamento ad esso associate, da cui dipendono, unitamente alla corrispondente amplificazione, gli effetti che il singolo modo è in grado di descrivere. Per poter cogliere con sufficiente approssimazione gli effetti dell’azione sismica sulla costruzione, è opportuno considerare tutti i modi con massa partecipante superiore al 5% e comunque un numero di modi la cui massa partecipante totale sia superiore all’85%, trascurando solo i modi di vibrare meno significativi in termini di massa partecipante. L’utilizzo dello spettro di risposta consente di calcolare gli effetti massimi del terremoto sulla costruzione associati a ciascun modo di vibrare. Tuttavia, poiché durante il terremoto gli effetti massimi associati ad un modo di vibrare non si verificano generalmente nello stesso istante in cui sono massimi quelli associati ad un altro modo di vibrare, tali effetti non possono essere combinati tra di loro mediante una semplice somma ma con specifiche regole di combinazione, di natura probabilistica, che tengono conto di questo sfasamento temporale. La regola di combinazione imposta nella norma è la regola di combinazione quadratica completa CQC (Complete Quadratic Combination): tale regola porta in conto anche l’eventuale correlazione tra i modi, attraverso il fattore ρ_ij. Essa degenera nella più semplice regola SRSS (Square Root of Sum of Squares), valida nell’ipotesi in cui i contributi massimi dei singoli modi non siano correlati e non si verifichino contemporaneamente. La SRSS può essere utilizzata, ove ritenuto necessario, come riferimento per il controllo dei risultati, tenendo presente che, in assenza di correlazione, la CQC degenera nella SRSS e che, in generale, quando il periodo di vibrazione di ciascun modo differisce di più del 10% da quello degli altri modi, le differenze tra le due regole diventano trascurabili.

C7.3.3.2 ANALISI LINEARE STATICA⁹
In letteratura e nei diversi documenti tecnici di riferimento esistono espressioni più o meno semplici per determinare, in maniera approssimata, il periodo del primo modo di vibrare della struttura, in ciascuna delle due direzioni principali.
L’equazione [7.3.6] della norma porta in conto, in maniera indiretta, l’effettiva rigidezza laterale della struttura e risulta, pertanto, più affidabile rispetto ad altre formulazioni più semplici, basate unicamente sul numero di piani o sull’altezza complessiva della costruzione, ma richiede necessariamente un modello di calcolo e un’analisi statica specifica.
Dipende dalle finalità dell’analisi il grado di approssimazione da conseguire nella determinazione del periodo T₁, cui è legata la risposta spettrale e quindi l’entità delle forze statiche equivalenti. In via di approssimazione, si può usare la seguente espressione semplificata:

dove H è l’altezza della costruzione, in metri, dal piano di fondazione e C₁ vale 0,085 per costruzioni con struttura a telaio di acciaio o di legno, 0,075 per costruzioni con struttura a telaio di calcestruzzo armato e 0,050 per costruzioni di muratura o per qualsiasi altro tipo di struttura.

⁹L’analisi lineare statica consiste sostanzialmente in un’analisi lineare dinamica semplificata in cui:
1) invece di effettuare l’analisi dinamica della costruzione si assume per essa un modo di vibrare principale avente un periodo T₁ calcolato in maniera approssimata (utilizzando l’espressione [7.3.6] delle NTC) e spostamenti linearmente crescenti con l’altezza dal piano di fondazione, ai quali corrisponde la distribuzione di forze statiche data dall’espressione [7.3.7] delle NTC. A questo modo di vibrare si associa un’aliquota λ di massa partecipante pari a 0,85 se la costruzione ha almeno tre orizzontamenti e se T₁ < 2T_C, pari a 1,0 in tutti gli altri casi;
2) si calcolano gli effetti dell’azione sismica, rappresentata dallo spettro di risposta di progetto, per il modo di vibrare principale considerato;
3) non si effettua alcuna combinazione degli effetti in quanto non si considerano altri modi di vibrare.

C7.3.4. ANALISI NON LINEARE DINAMICA O STATICA
C7.3.4.1 ANALISI NON LINEARE DINAMICA
Per eseguire analisi non lineari dinamiche occorre definire da un lato un modello della struttura che descriva opportunamente le fonti di non linearità significative, dall’altro le storie temporali di accelerazioni che descrivono il moto del terreno. Ciascuna storia temporale (accelerogramma) descrive una componente, orizzontale o verticale, dell’azione sismica; l’insieme delle tre componenti (due orizzontali, tra loro ortogonali, e una verticale) costituisce un gruppo di storie temporali del moto del terreno.  Gli accelerogrammi possono essere artificiali, naturali o simulati e devono essere opportunamente selezionati e scalati, secondo quanto indicato nel § 3.2.3.6 e nel § C3.2.3.6.
Nelle analisi non lineari con integrazioni al passo, un punto cruciale, oltre alla selezione degli accelerogrammi, è rappresentato dalla scelta delle direzioni di applicazione dell’input sismico rispetto alle direzioni principali della struttura.
A questo scopo, per gli accelerogrammi naturali, può essere utile proiettare ciascuna coppia di registrazioni lungo le direzioni principali del sisma, come indicato al § C3.2.3.6.
I modelli da utilizzare per effettuare analisi non lineari dinamiche devono rispettare i requisiti del § 7.2.6 delle NTC. In particolare essi devono consentire una corretta rappresentazione degli elementi strutturali in termini di rigidezza, resistenza, e di comportamento post-elastico, devono rappresentare correttamente la capacità dissipativa per isteresi e i possibili fenomeni di degrado associati alle deformazioni cicliche. Un punto cruciale, nelle analisi non lineari dinamiche, è rappresentato dalla adeguata definizione della matrice di smorzamento.
La norma richiede espressamente il confronto tra i risultati dell’analisi dinamica non lineare e quelli dell’analisi modale con spettro di progetto, in termini di sollecitazioni globali alla base della struttura. Tale confronto deve fornire risultati coerenti, in generale spiegabili attraverso il fattore di comportamento o, in caso contrario, attraverso l’interpretazione della risposta della struttura e dei meccanismi inelastici evidenziati dalle analisi non lineari.

C7.3.4.2 ANALISI NON LINEARE STATICA
L’analisi non lineare statica consente di determinare la curva di capacità della struttura, espressa dalla relazione F_b-d_c, in cui F_b è il taglio alla base e d_c lo spostamento di un punto di controllo, che per gli edifici è in genere rappresentato dal centro di massa dell’ultimo orizzontamento. Per ogni stato limite considerato, il confronto tra la curva di capacità e la domanda di spostamento consente di determinare il livello di prestazione raggiunto. A tal fine, abitualmente, si associa al sistema strutturale reale un sistema strutturale equivalente a un grado di libertà.
Figura C7.3.1 – Sistema e diagramma bilineare equivalente

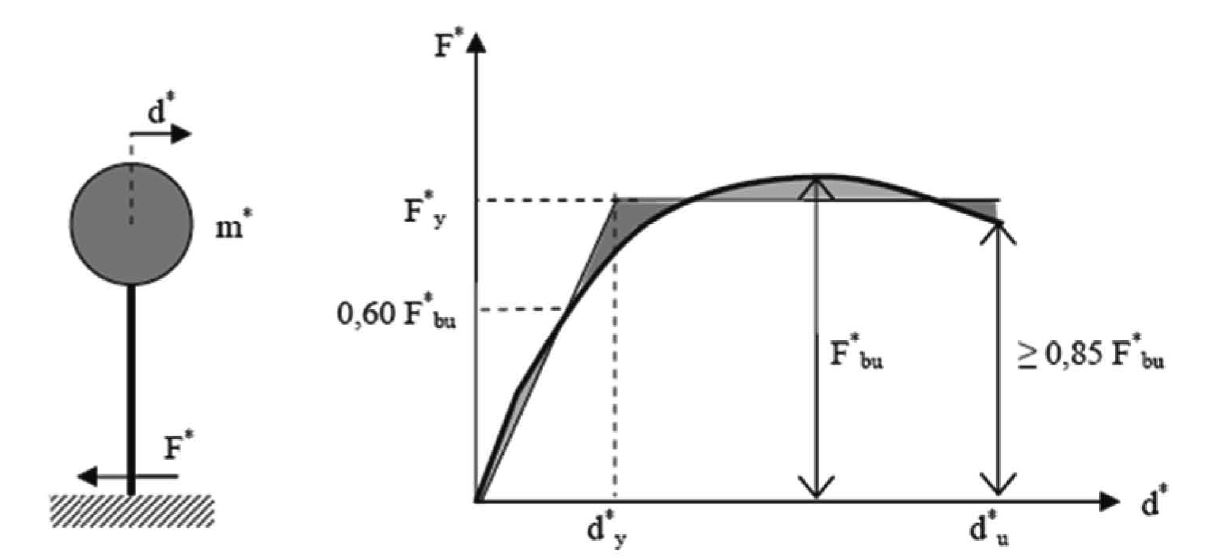
La forza F* e lo spostamento d* del sistema equivalente sono legati alle corrispondenti grandezze F_b e d_c del sistema reale dalle relazioni:


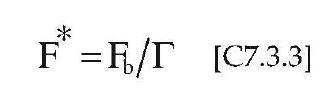
Dove Γ è il “fattore di partecipazione modale” definito dalla relazione:

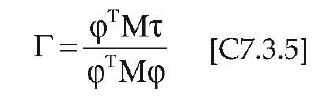
Il vettore τ è il vettore di trascinamento corrispondente alla direzione del sisma considerata; il vettore φ è il modo di vibrare fondamentale del sistema reale normalizzato ponendo d_c = 1; la matrice M è la matrice di massa del sistema reale.
Ai fini operativi, per poter determinare in forma chiusa l’energia dissipata dal sistema e, quindi, lo smorzamento equivalente, alla curva di capacità del sistema equivalente è utile sostituire una curva bilineare. Le tecniche di bilinearizzazione si basano usualmente su principi di equivalenza energetica, imponendo che le aree sottese alla curva bilineare e dalla curva F*-d* siano uguali.
Per la valutazione del punto di prestazione (PP) della struttura è possibile seguire uno dei seguenti metodi:
- metodo A, basato sull’individuazione della domanda anelastica attraverso il principio di uguali spostamenti o uguale energia.
- metodo B, basato sulla costruzione di uno spettro di capacità.

Metodo A
Alla curva di capacità del sistema equivalente si sostituisce una curva bilineare avente un primo tratto elastico ed un secondo tratto perfettamente plastico (si veda Figura C7.3.1). Detta F_bu la resistenza massima del sistema strutturale reale ed F*_bu = F_bu / Γ la resistenza massima del sistema equivalente, il tratto elastico si individua imponendone il passaggio per il punto 0.6F*_bu della curva di capacità del sistema equivalente, la forza di plasticizzazione F*_y si individua imponendo l’uguaglianza delle aree sottese dalla curva bilineare e dalla curva di capacità per lo spostamento massimo d*u corrispondente ad una riduzione di resistenza ≤ 0.15 F*_bu.
Il periodo elastico del sistema bilineare è dato dall’espressione:

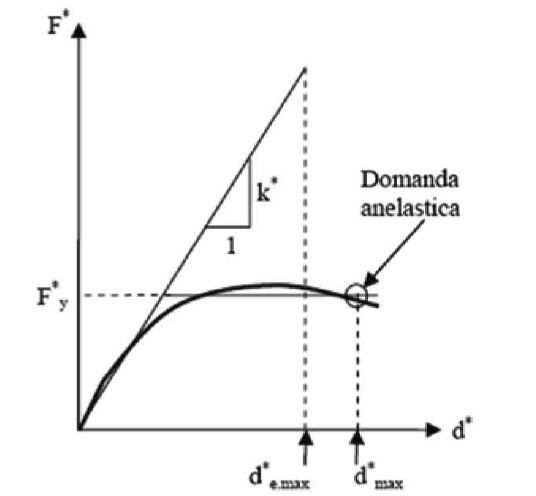
Nel caso in cui T*≥ T_C la domanda in spostamento per il sistema anelastico è maggiore di quella di un sistema elastico di pari periodo (v. § 3.2.3.2.3 delle NTC e Figura C7.3.2a):

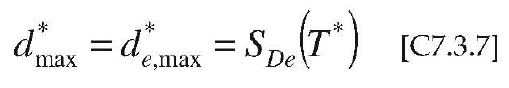
Nel caso in cui T*< T_C la domanda in spostamento per il sistema anelastico è maggiore di quella di un sistema elastico di pari periodo (v. Figura C7.3.2b) e si ottiene da quest’ultima mediante l’espressione:

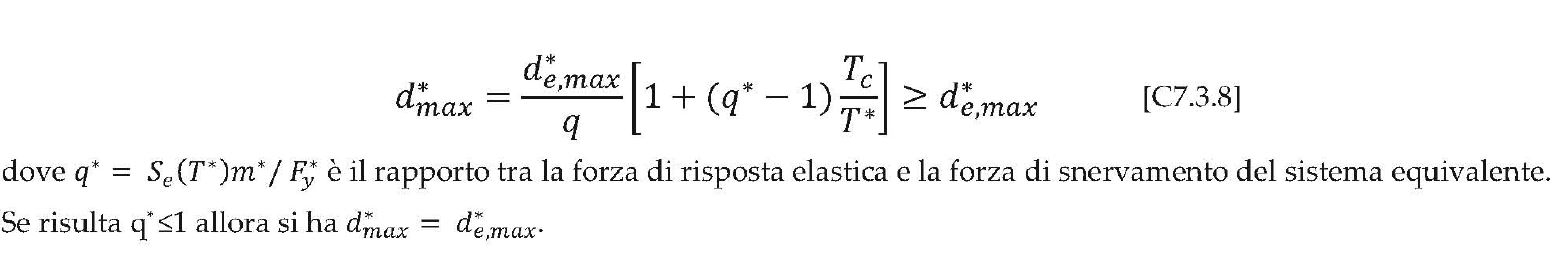
Figura C7.3.2a – Spostamento di riferimento per T*≥ T_C

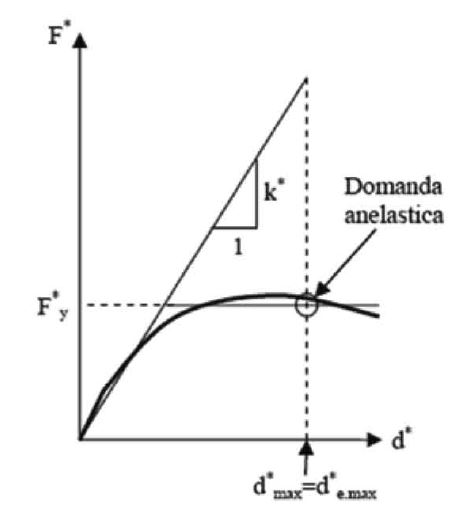
Figura C7.3.2b – Spostamento di riferimento per T*< T_C

Metodo B
In questo metodo il punto di prestazione e lo spostamento atteso per un dato livello di azione sono valutati attraverso un processo iterativo.
Si converte lo spettro di domanda nel relativo spettro sul piano ADRS, in cui le accelerazioni spettrali Se sono rappresentate in funzione degli spostamenti spettrali S_De, ottenuti attraverso l’espressione [3.2.10] delle NTC.
Si effettua una prima stima del punto di prestazione ipotizzando, generalmente, che lo spostamento d*_max sia pari a quello di una struttura elastica avente la stessa rigidezza iniziale della struttura analizzata:

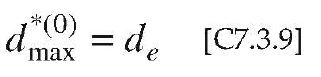
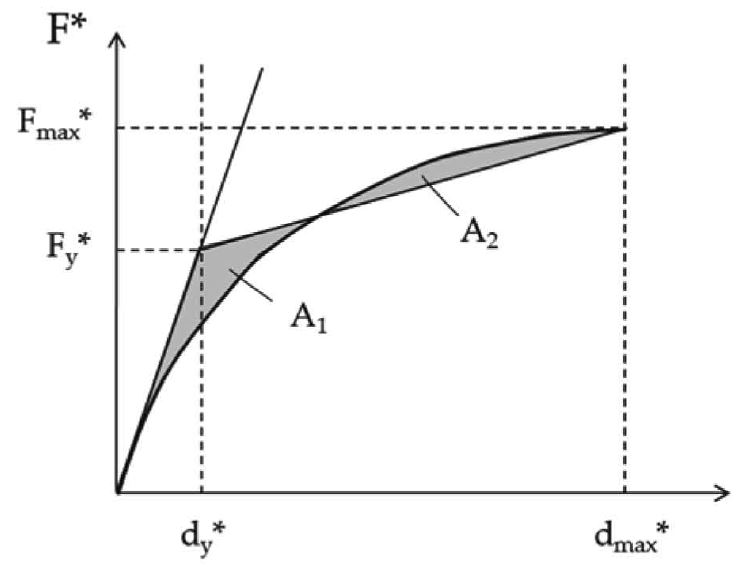
Stimato il punto di prestazione (F_max*, d_max*) sulla curva di capacità del sistema equivalente F*-d*, ad essa si sostituisce una curva bilineare equivalente, in termini energetici, ottenuta adottando un primo tratto con pendenza pari alla rigidezza iniziale della struttura ed identificando la forza F_y* e la pendenza del tratto F_y*-d_max* imponendo l’uguaglianza dell’area sottesa dalle due curve, come mostrato in Figura C7.3.3. Per rappresentare la curva bilineare F*-d* sul piano ADRS, occorre dividere le forze per m*.
Figura C7.3.3 – Bilinearizzazione equivalente

A partire dalla curva bilinearizzata così definita, si calcola lo smorzamento viscoso equivalente associato, espresso in percentuale, attraverso la [C7.3.10]:

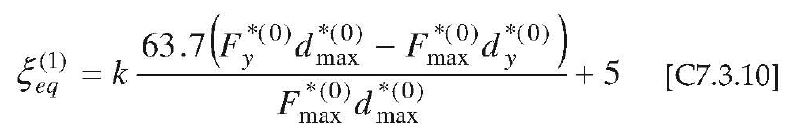
dove il coefficiente k tiene conto della capacità dissipative della struttura ed in particolare delle caratteristiche del ciclo di isteresi.
Indicativamente, si possono assumere i seguenti valori, a seconda della differente tipologia strutturale:
- strutture a elevata capacità dissipativa (caratterizzate da cicli di isteresi stabili e ragionevolmente ampi): k=1;
- strutture a moderata capacità dissipativa (caratterizzate da cicli di isteresi con moderata riduzione dell’area): k= 0,66;
- strutture a bassa capacità dissipativa (caratterizzate da cicli di isteresi con pinching elevato e da una sostanziale riduzione dell’area): k=0,33;
- strutture dotate di appositi dispositivi di dissipazione: va valutata l’energia dissipata complessivamente, attribuendo alla struttura e al sistema di dissipazione il valore di k corrispondente all’effettiva capacità di dissipazione.
Grazie al coefficiente ξ_eq così calcolato si abbatte, utilizzando l’espressione [3.2.4] delle NTC, lo spettro di domanda.
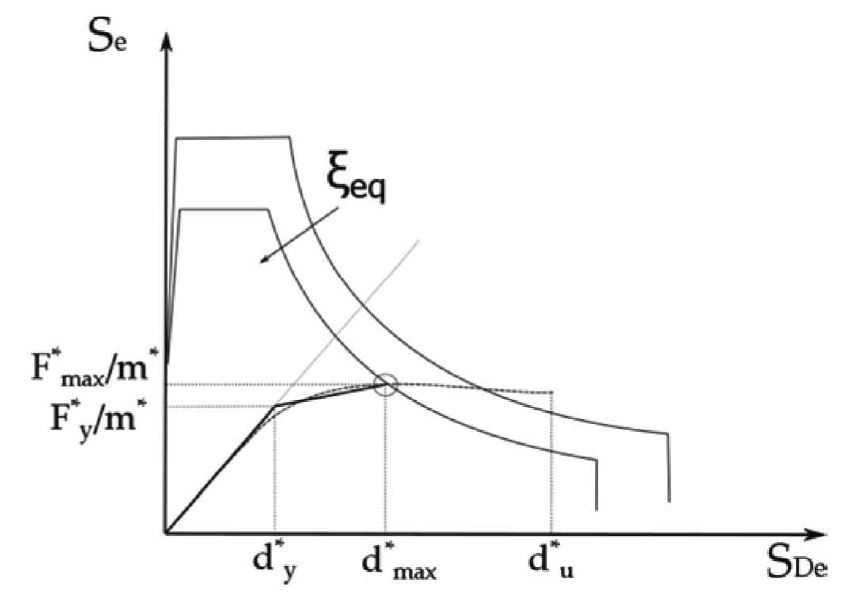
L’intersezione, sul piano ADRS, fra lo spettro di domanda abbattuto e la curva di capacità del sistema equivalente fornisce il nuovo punto di prestazione, come mostrato in Figura C7.3.4; se esso è caratterizzato da uno spostamento d*⁽¹⁾_max ragionevolmente prossimo a quello stimato in partenza d*⁽⁰⁾_max, la procedura iterativa ha termine e si ha la soluzione.
Figura C7.3.4 – Individuazione del Punto di prestazione

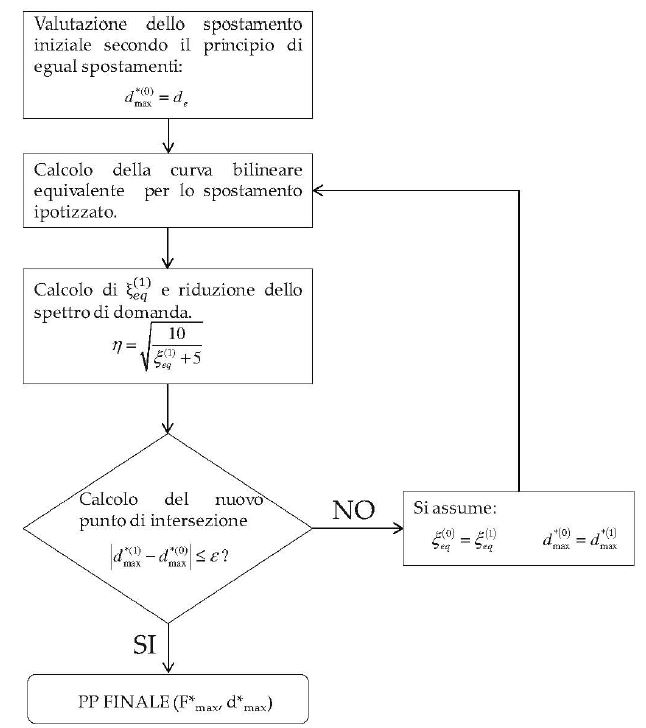
La procedura, iterativa, è ripetuta fino a convergenza della soluzione, entro la tolleranza stabilita, secondo lo schema di Figura C7.3.5.
Figura C7.3.5 – Diagramma di flusso per la procedura iterativa di ricerca del punto di prestazione

Una volta trovata la domanda di spostamento d*_max, per lo stato limite in esame si verifica la compatibilità degli spostamenti, per gli elementi/meccanismi duttili, e delle resistenze, per gli elementi/meccanismi fragili.
L’analisi non lineare statica, condotta nei modi previsti dalle NTC, può sottostimare significativamente le deformazioni sui lati più rigidi e resistenti di strutture flessibili torsionalmente, cioè strutture in cui il modo di vibrare torsionale abbia un periodo superiore ad almeno uno dei modi di vibrare principali traslazionali. Per tener conto di questo effetto, tra le distribuzioni secondarie delle forze occorre scegliere la distribuzione adattiva.
Per ciascuna direzione, devono essere eseguite due analisi distinte, applicando l’azione sismica in entrambi i possibili versi e considerando gli effetti più sfavorevoli derivanti da ciascuna delle due analisi.

C7.3.5. RISPOSTA ALLE DIVERSE COMPONENTI DELL’AZIONE SISMICA ED ALLA VARIABILITÀ SPAZIALE DEL MOTO
Nel caso di analisi statiche non lineari è possibile applicare separatamente ciascuna delle due componenti orizzontali (insieme a quella verticale ove necessario ed agli spostamenti relativi prodotti dalla variabilità spaziale del moto ove necessario), riconducendo quindi la valutazione unitaria degli effetti massimi ai valori più sfavorevoli così ottenuti.
Quando la variabilità spaziale del moto può avere effetti significativi sulla risposta strutturale essa deve essere considerata.
In generale l’effetto principale della variabilità è dovuto ai notevoli spostamenti relativi che essa genera alla base delle strutture, mentre la risposta dinamica risulta inferiore a quella ottenuta con moto sincrono. In questi casi risulta pertanto cautelativa la valutazione della risposta sovrapponendo l’effetto della distorsione degli appoggi a terra alla risposta all’azione sincrona, come indicato al punto 3.2.4.
Qualora si utilizzi l’analisi non lineare si potranno cautelativamente imporre le distorsioni alla base ed effettuare l’analisi dinamica sincrona.
In alternativa è possibile imporre alla base della costruzione serie temporali del moto sismico differenziate ma coerenti tra loro, in accordo con le caratteristiche dei siti ove sono situati i punti di appoggio della costruzione.
Quest’ultimo criterio, apparentemente più rigoroso, presentando difficoltà operative nella effettiva definizione delle storie temporali, richiede una notevole cautela da parte del progettista.
In ogni caso si deve considerare anche la risposta al moto sincrono.

C7.3.6. RISPETTO DEI REQUISITI NEI CONFRONTI DEGLI STATI LIMITE
In generale, la progettazione ha un’articolazione di tipo multi-prestazionale e multi-strategico. I diversi livelli prestazionali sono associati ai diversi stati limite, mentre le diverse strategie sono associate alla destinazione d’uso della costruzione.
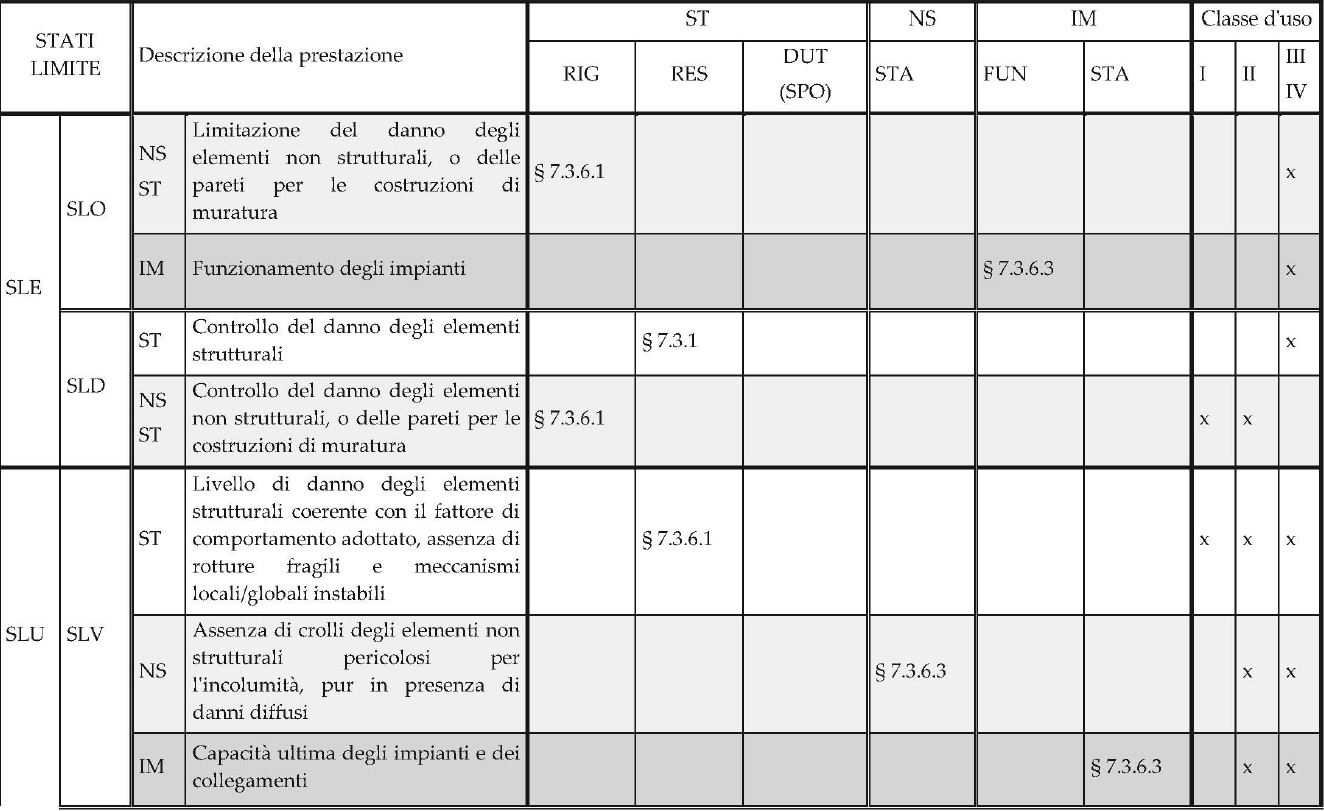
La Tab. 7.3.III della norma sintetizza le diverse verifiche da eseguire per le costruzioni a comportamento dissipativo; nella Tabella C7.3.I, si esplicitano con maggiore dettaglio le verifiche riportate nella Tabella 7.3.III della norma, fornendo anche una descrizione sintetica della prestazione associata a ciascuno stato limite e indicando, per ogni elemento costruttivo, il riferimento al paragrafo della norma a cui si riferisce ciascuna delle verifiche.
La tabella C7.3.I fornisce, per ciascuno Stato Limite e per ciascun tipo di elemento (strutturale, non strutturale o impianto), la descrizione delle prestazioni in termini di danno, capacità ultima (resistenza o duttilità) o funzionamento; essa indica, inoltre, il tipo di verifica, in termini di confronto tra capacità e domanda, e il tipo di elemento su cui la verifica deve essere eseguita, per soddisfare il requisito prestazionale dato.
Tabella C7.3.I – Stati Limite di elementi strutturali primari, elementi non strutturali e impianti: descrizione delle prestazioni e corrispondenti verifiche

C7.3.6.1 ELEMENTI STRUTTURALI (ST)
Nelle verifiche di cui al § 7.3.6.1, nel caso di analisi lineari (§ 7.3.3.) si assume d_r = d_Ee.¹⁰
In merito alle “Verifiche di Rigidezza (RIG)”, per le tamponature duttili di cui al punto a) e per le tamponature di cui al punto b), va verificato sperimentalmente che il raggiungimento dei rispettivi limiti di interpiano 0,0075h e 0,0100h siano ottenuti sulla parte ascendente della curva di comportamento Forza-Spostamento relativo, oppure sul ramo discendente verificando però che la perdita di resistenza sia inferiore al 10% del massimo. Inoltre, durante la prova non si dovranno riscontrare significativi danneggiamenti sugli elementi.
Per tamponature duttili si intendono elementi non strutturali che sviluppano un comportamento plastico o incrudente al di là del limite elastico e deformazioni significativamente maggiori delle deformazioni al limite elastico.

¹⁰Le verifiche sugli elementi strutturali si eseguono in termini di:
- rigidezza, per contenere le deformazioni indotte dal sisma e conseguentemente i danni sugli elementi non strutturali;
- resistenza, per soddisfare la domanda allo SLV, in condizioni ultime o sostanzialmente elastiche, a seconda che si faccia riferimento a un comportamento strutturale dissipativo o non dissipativo;
- duttilità, per garantire alla struttura la capacità di sostenere la domanda di spostamento allo SLC.
Relativamente all’ultimo dei tre punti sopra elencati, per le strutture a telaio o a pareti, oltre ai dettagli costruttivi, sono previste specifiche verifiche di duttilità che riguardano gli elementi verticali primari allo spiccato delle fondazioni e per tutte le zone dissipative degli elementi strutturali secondari.

C7.3.6.2 ELEMENTI NON STRUTTURALI (NS)
Il controllo del danno negli elementi non strutturali si effettua, in maniera indiretta, intervenendo sulla rigidezza degli elementi strutturali al fine di contenere gli spostamenti di interpiano, come indicato al § 7.3.6.1. Devono essere eseguite invece verifiche dirette in termini di stabilità. La prestazione, consistente nell’evitare la possibile espulsione delle tamponature sotto l’azione della F_a, si può ritenere conseguita con l’inserimento di leggere reti da intonaco sui due lati della muratura, collegate tra loro ed alle strutture circostanti a distanza non superiore a 500 mm sia in direzione orizzontale sia in direzione verticale, ovvero con l’inserimento di elementi di armatura orizzontale nei letti di malta, a distanza non superiore a 500 mm. La domanda sismica F_a si determina secondo le indicazioni del § 7.2.3 della norma e del § C7.2.3.